Notes on the School of Batman Podcast
Published:
I was featured on the (all around cool and intriguing) podcast School of Batman to talk about my field, chemistry, the subfield of my research group, quantum chemistry, and my own specialization, machine learning in quantum chemistry. I made this post to give some clarifications, expansions, and visualizations on things I talked about. I will go through it chronologically. You can find the podcast here or directly here:
In a Nutshell
When I think of ‘lab chemistry’, I usually have a synthetical chemist in mind who produces molecules that can be used for a wide variety of tasks like glue, pesticides, plastics or drugs. In the podcast, I use drugs to illustrate my points. An organic chemist might have a procedure like the following:
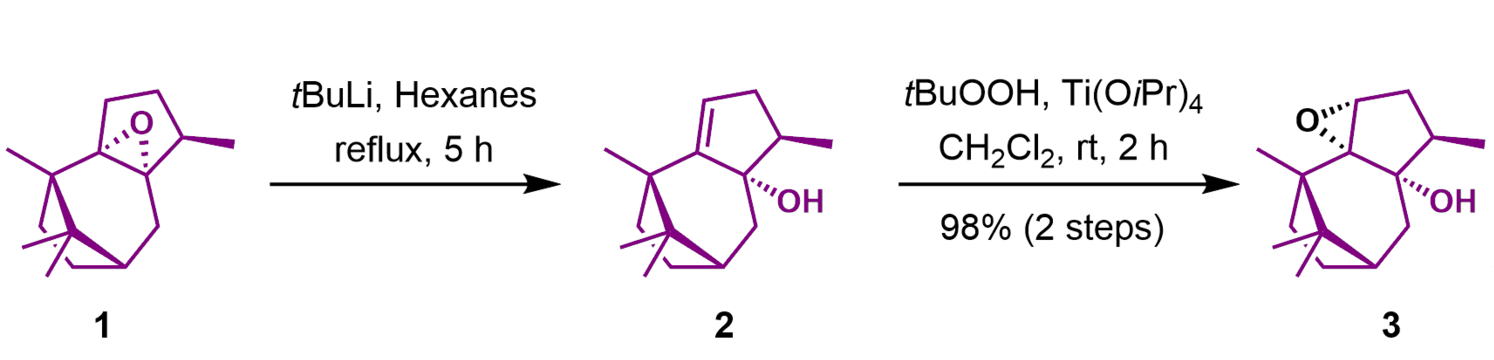
This is part of the first route ever described to synthesize Taxol aka Paclitaxel, a drug for chemotherapy. The chemists actually stand at their benches and put chemical 1 in a flask and add t-BuLi and hexane, two reagents, and cook (‘reflux’) it for 5 h and so on and so on. You see this takes a lot of time to prepare, especially if you are the first person ever to try it. A lot of dead ends are to be expected. Despite me just glossing over it, this is an enormously difficult and tedious process: A lot of practical knowledge is required to ‘cook’ your molecule but you also need to be on top of theory to draw up a synthesis like the one shown here – just usually with many, many more steps.
In theoretical chemistry (which is sometimes used synonymously with quantum chemistry) what we work with looks more like this:
\[i \hbar \frac{d}{d t}\vert\Psi(t)\rangle = \hat H\vert\Psi(t)\rangle\]which is called the Schrödinger Equation, which is at the basis for most of most theoretical chemistry. By solving it, we can find properties of molecules without actually synthesizing them. It is extremely time consuming to find a solution for this equation for larger molecules like Taxol above. There is an even more accurate equation that also takes into account Einstein’s theories (it’s called the Dirac equation, but you guessed it: it takes even more time to solve it. And when I say ‘solve it’, I mean – in all but the most simple cases – ‘find an approximate solution.’ There are many ways to find calculation shortcuts, e.g. by restricting the equation just to one class of molecules (for instance drug-like molecules). The shortcut I focus on is machine learning, which is, broadly speaking, a set of statistical methods. Another shortcut is molecular dynamics (‘simulate molecules’), which I will explain a bit more below.
Drug Development 
In drug discovery, during the very first phase of finding a new drug, thousands of molecules will be synthesized and tested with high-throughput screening. Machines and humans systematically produce new molecules and test them for desired properties. After a process that may take up to 5 years, the first molecules will be tested in living organisms and only then in humans (‘clinical trials’). As you can imagine, this costs a boatload of money. One way to cut these costs might be machine learning and virtual screening, where a vast number of molecules don’t have to be synthesized because we can already theoretically predict that they might be toxic or that they don’t show a desired property. After listing all the properties them, we might see some of them cluster together, except we don’t because high dimensional space (e.g. 1000-dimensional space) is not really human readable. A computer analysis might find something like this, where a molecule is clustered according to some internal angles:

It’s immediately clear that millions of compounds can’t really be handled well on neither your average laptop nor by any human. This is where machine learning and supercomputers come to the rescue! To play around with molecule clusters, you should try out sketchmap.
Machine Learning and a Bit of AI History
I used the phrase ‘neural winter’ in the podcast yet in the literature you would rather read about the ‘AI winter’. I use it synonymously to denote a period starting from the 70’s and peaking in early 90’s where funding for AI was sparse and people were rather pessimistic about progress in AI. Commonly it is even subdivided into the first (1974–1980) and second (1987–1993) AI winter. I extracted all year numbers mentioned in the Wikipedia article on the history of AI and plotted them in the following. Of course this is highly dependent on how the article was written – it’s nonetheless satisfying to see that the years within the neural winters produced less Wikipedia relevant output than the others:
As you can see in the figure above, the neural winter was preceded by the ‘golden years’. At latest in 2012, machine learning and AI were back on track with successful applications of neural nets and deep learning for a host of problems. These applications range from impressive but not straightforwardly applicable ones like the program that plays the board game Go, to industrial applications like Google’s algorithm that shows you YouTube videos, to more humanitarian and basic research ones like Google’s algorithm that detects eye diseases. All three examples here are related to Google, one of the major driving forces in the field, be it industrial or research-wise. Currently, AI and machine learning are revolutionizing large parts of the industry, reminiscent of when the introduction of the personal computer turned over many businesses. A full history on AI is found on Wikipedia and gives a decent overview.
Pople and Early Computational Chemistry
John Pople was one of the fathers of computational chemistry proper with the development of the quantum chemical software Gaussian. (On a tangent: The course of Gaussian became pretty weird after people got ‘banned’ from using it, even Pople himself was banned). It remains one of the most cited programs in academia and has had enormous influence on how we go about with more modern iterations of quantum software. He won the Nobel Prize in 1998 and he died in 2004, aged 78.

The computational chemistry we are talking here is all quantum. Unlike molecular dynamics, which applies Newtonian forces to all the atoms, in quantum chemistry we assume all the atoms behave in a ‘quantum way’. Without going into the details of quantum mechanics, for us it mainly means that the electrons behave in a very complicated way, which in turn results in long computing time. The Newtonian picture ignores electrons and is therefore much faster for molecules of the same size, yet much less accurate, because the world is (likely) fundamentally quantum (that’s why I was calling molecular dynamics a shortcut above: it utilizes the Newtonian approximation (to speed up the calculations)). When we want to check out really large molecules like proteins, we adapt the Newtonian picture, because a quantum calculation could take millions of years. Here is a very small protein as illustration. It’s gramicidin S, an antibiotic.
It has 174 atoms. When we compare that to the tiny H2O molecule, which has only 3 atoms, it seems huge. If H2O is a big deal to calculate, you can imagine how difficult gramicidin S is. The largest protein known is Titin (a human adult has about 0.5 kg of Titin in their muscles) with up to 539,022 atoms (depending on which variant).
Batman’s case
So what would be needed for Batman’s case of children being manipulated by a drug is a forensic chemist. Apart from the analytical methods used in this field, I’m not very familiar with the specifics. Of course, a theoretician is not immediately useful at a crime scene like the one described in the podcast. Machine learning has helped in many branches of analytical chemistry so indirectly algorithms and methods that I might develop could maybe perhaps help Batman at some point. Figuring out what kind of poison the children ingested seems to be a good starting point.
Back to Neural Networks
What I am trying to say a bit haphazardly in the podcast is the following: Up to 2012 (or so), stuff you wanted to classify like birds or handwriting had to follow a very clear form to be interpretable for a program. This form could be a checklist: Does it have a beak? ![]() Does it have feathers?
Does it have feathers? ![]() Does it lay eggs?
Does it lay eggs? ![]() If it fulfills all these criteria, it is a bird, else it isn’t. The problem is that for most things it is very difficult to list all properties and you are almost guaranteed to miss some. What if we were to find a featherless bird (like a hatchling). Or a non-bird that fulfills all the criteria. A neural network is able to generalize a bird so much that it can learn about birds without having a bunch of specific yes/no questions, but it could classify birds just by looking at pictures, just like humans. In fact, as of 2015, machines classify images better (and of course faster) than humans.
If it fulfills all these criteria, it is a bird, else it isn’t. The problem is that for most things it is very difficult to list all properties and you are almost guaranteed to miss some. What if we were to find a featherless bird (like a hatchling). Or a non-bird that fulfills all the criteria. A neural network is able to generalize a bird so much that it can learn about birds without having a bunch of specific yes/no questions, but it could classify birds just by looking at pictures, just like humans. In fact, as of 2015, machines classify images better (and of course faster) than humans.
Neural networks are inspired by how nature processes information. The human brain is of course far away from being modeled or simulated but we still managed to figure out how to upload aspects of a worm’s brain into a LEGO robot. This video complements what I say in the podcast quite nicely:
The worm has to make certain decisions during its life. The decision food/light vs. food/non-light vs. non-food/light vs. non-food/non-light is important for the worm’s survival, so the ‘brain’ of the worm developed a classifier for these food/light combinations. Instead of ‘thinking’ about food and light, we could change it (as soon as we have a model of that brain on the computer) in a way to classify birds along beak/feathers vs. non-beak/feathers, … etc. If we make the neural net large enough (much larger and more connected than in a worm, which is then called deep learning), it can do all the many fascinating things mentioned before. Size is not everything for a potent algorithm but it seems pretty important. Active research studies different ways to structure the neural nets instead of just making them larger.
Wrapping it up
In the end of the podcast, I talk probability. One cool thing that machine learning brought to chemistry is talking about probabilities and uncertainties. Whenever we do an estimate, we want to know how certain we are (turns out, usually we’re not very certain). If you’ve ever watched Jeopardy! with IBM Watson, the AI program that answers Jeopardy! questions, you could’ve seen something like this:

Of course, Watson knows the answer. But we see that he wasn’t entirely sure. There is always a bit of uncertainty remaining (in humans, this manifests itself usually as epistemic humility (or arrogance/overconfidence, if we are never uncertain)). With the example from the podcast: A program might never be 100 % sure that something is a bird and will always have some residual doubt whether it might be something else (e.g. a hippogriff).
I was a bit all over the place in the end of the podcast. I just wanted to say that we can figure out properties of molecules and they could be understood in the analogy as beaks or wings of an animal, which are properties that let us identify the animal as a bird.
Again it was very cool to take part and I hope I could clarify some things here. Stay tuned for more.
